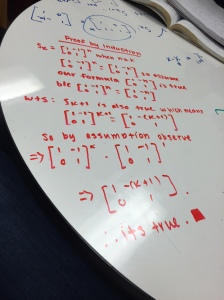The One Where We Get Funky (Nov. 9)

December 3, 2015 / tripletintegral / Leave a comment

I’m still soooooo behind, but I am trying to get all caught up!!!

Today we started to talk about functions which are “funky relations.”

A function is defined as, ${f}:{A}\rightarrow{B}$ , is a relation, ${f}\subseteq{AxB}$ such that $\forall{a}\in{A},\exists!b\in{B}, (a,b)\in{f}$ . In essence, ${f}:{A}\rightarrow{B}$ is a well-defined rule that associates to every ${a}\in{A}$ some ${b}\in{B}. Or, to put it in even simpler terms,$ latex {f}({a})={b}$.

Recalling a blast from the past, remember that for something to be a function it must pass the vertical line test. This would mean that the following is not an example of a function:

${f}=\leftbrace{(x,y)}:{x}^{2}+{y}^{2}={1}\rightbrace\subseteq\mathbb{R}{x}\mathbb{R}$
$(0,1)\in{f}$
$(0,-1)\in{f}$ , which violates the vertical line test.

We then discussed the domain and co-domain of functions. The domain of ${f}$ is represented by ${A}$ whereas the co-domain is represented by ${B}$ . In more mathy language:

${A]=\text{the domain of f}\Rightarrow\forall{a}\in{A},f(a)\in{B}$ .

${B}=\text{the co-domain of f}\Rightarrow\text{it's not necessarily true that every b}\in\{B}\text{ is an output. However, all of f's outputs live in B.}$

We then went over some important definitions:

Definition 1: Two functions ${f}:{A}\rightarrow{B}$ and ${g}:{C}\rightarrow{D}$ are equal if:

1) A = C
2) B = D
3) f = g

Definition 2: A function, ${f}:{A}\rightarrow{B}$ ,is said to be surjective/epic/onto if $\forall{b}\in{B},\exists{a}\in{A},f(a)={b}$ .

Definition 3: A function, ${f}:{A}\rightarrow{B}$ is called injective/monic/one-to-one if: $({a}_{1}\neq{a}_{2})\Rightarrow{(f({a}_{1}\eq{f({a}_{2}))$

*****NOTE: When proving this it easier to prove the contrapositive: ${(f({a}_{1}))\eq{f({a}_{2}))\Rightarrow{({a}_{1}\eq{a}_{2})$ .

Definition 4: A function, ${f}:{A}\rightarrow{B}$ that is both surjective and injective is consider bijective.

The One With Partitions and Well-Defined Things (Nov. 6)

November 16, 2015November 16, 2015 / tripletintegral / Leave a comment

Today was a lecture heavy day, so we have quite a bit of notes from today. The main ideas we went over were partitions, which were briefly discussed on Nov. 2.

Theorem: An equivalence relation, $\mathrm{R}$ on a set $\mathrm{A}$ can be used to partition $\mathrm{A}$ into equivalence classes.

Proof: Suppose $\mathrm{R}$ is an equivalence relation on $\mathrm{A}$ . We need to show that $\{[\mathrm{a}] : \mathrm{a}\in\mathrm{A}\} = \mathrm{A}/\sim$ is a partition for $\mathrm{A}$ . In order for this to be true, the union of all equivalence class should equal $\mathrm{A}$ .

i.e. $\bigcup_{\mathrm{a}\in\mathrm{A}}[\mathrm{a}] = \mathrm{A}$

It must also be true that the intersection of any two distance equivalence classes is the empty set and that no equivalence class is the empty set.

Since $\mathrm{R}$ is an equivalence class, we know that by definition $\mathrm{R}$ is reflexive. This means that $\forall\mathrm{a}\in\mathrm{A},\mathrm{a}\in\[\mathrm{a}]\Rightarrow[\mathrm{a}]=\text{empty set}$ .

Suppose $[\mathrm{a}] \cap[\mathrm{b}]\neq\emptyset$ . This means $\exists\mathrm{x}\in\mathrm{A}, \mathrm{x}\in[\mathrm{a}]$ and $\mathrm{x}\in[\mathrm{b}]$ . Hence, $\mathrm{xRa}\text{and}\mathrm{xRb}$ the tells us that by symmetry we have $\mathrm{x}~\mathrm{a}\text{and}\mathrm{x}~\mathrm{b}$ which through transitivity implies that $\mathrm{a}~\mathrm{b}$ .

Now, let $\mathrm{y}\in[\mathrm{a}]\Rightarrow\mathrm{y}~\mathrm{a}\Rightarrow\mathrm{y}~\mathrm{b}\Rightarrow\mathrm{y}\in[\mathrm{b}]$ . As a result, $[\mathrm{a}]\subseteq[\mathrm{b} Now, let$ latex \mathrm{z}\in[\mathrm{b}]\Rightarrow\mathrm{z}~\mathrm{b}$
$\mathrm{z}~\mathrm{a}$ (transitivity)
$\Rightarrow\mathrm{z}\in[\mathrm{a}]$
$\Rightarrow[\mathrm{b}]=[\mathrm{a}]$

To show that $\bigcup_{\mathrm{a}\in\mathrm{A}}[\mathrm{a}]=\mathrm{A}$ we will argue two implications:

(1) $\bigcup_{\mathrm{a}\in\mathrm{A}}[\mathrm{a}]\subseteq\mathrm{A}$
(2) $\bigcup_{\mathrm{a}\in\mathrm{A}}\supseteq\mathrm{A}$

(1) Let $\mathrm{x}\in\bigcup_{\mathrm{a}\in\mathrm{A}}[\mathrm{a}]$ . This means that $\mathrm{x}~\mathrm{a}$ for some $\mathrm{a}\in\mathrm{A}$ . In essence, $\mathrm{x}\in[\mathrm{a}]=\{\mathrm{w}\in\mathrm{A}:\mathrm{w}~\mathrm{a}\}$
$\Rightarrow\mathrm{x}\in\mathrm{A}$
Hence, $\bigcup_{\mathrm{a}\in\mathrm{A}}[\mathrm{a}]\subseteq\mathrm{A}$

(2) Let $\mathrm{y}\in\mathrm{A}$ . Since $\mathrm{R}$ is reflexive, $\mathrm{y}~\mathrm{y}\Rightarrow\mathrm{y}\in[\mathrm{y}]\Rightarrow\mathrm{y}\in\bigcup_{\mathrm{a}\in\mathrm{A}}[\mathrm{a}]$ . $\square$

We then discussed what it means for something to be well-defined. This is best shown with examples of what it is and is not. We started with an example of what well-defined is not:

$\mathrm{S}=\{\text{all polynomials with real coefficents}\}$
$\Rightarrow\mathrm{f(x) \sim g(x)}\text{ if deg f = deg g}$
$\mathrm{S}$ is partitioned by $\{[\text{ deg 0}], [\text{deg 1 }], \text{...}\}$
$\Rightarrow \mathrm{S} = \{ [2], [\mathrm{x}], [\mathrm{x}^{2}], \text{...}\}$

Notice that there are several ways in which this can be written out:

$[2] + [\mathrm{x}] = [2 + \mathrm{x}]$ which is degree equivalent with:
$[2] + [5\mathrm{x}] = [2 + 5\mathrm{x}]$

That means that our set is not well-defined. Now for an example of what well-defined actually is:

$\mathrm{A} = \mathbb{Z}, \mathrm{x}~\mathrm{y}\text{ if }\mathrm{x}\equiv\mathrm{y}\text{mod}{4}, \mathbb{Z}/ = \{[0], [1], [2], [3]\}$

Apparently, well-defined will come back in Abstract Algebra when we study groups that are sets that use operations to combine stuff.

Peace
Emily

The One With Homework and the POW (Nov. 4)

November 16, 2015 / tripletintegral / Leave a comment

This class was fairly uneventful, we just worked on the problem of the week and the homework that was due this week, so I don’t really have much to say about it. I would blog about the homework, but I’ve already turned it in and haven’t gotten the grade back yet so yeah…I don’t really feel like redoing the homework I’ve already done. So, instead here are some cool Lego pictures from the Internet!

Peace
Emily

The One With The Wiggles (Nov. 2)

November 15, 2015November 15, 2015 / tripletintegral / Leave a comment

Today we learned about a term most commonly referred to as “wiggles”, which of course led to a discussion on the kids’ show The Wiggles. That made me think of this video of theirs that I really liked as a kid, but now just makes me feel like I’m on drugs.

Wiggles, which is notated as ” ~ “, is just and easier way of saying and notating that something relates to something else. So if you said ” a wiggles b” you would really being saying that ” a is related to b. ” Here are some examples of how to use this notation:

(1) Equiv. Classes : $[\mathrm{a}] = \{\mathrm{x}\in\mathrm{A} : \mathrm{x} ~ \mathrm{a}\}$
(2) Reflexivity : $\mathrm{x} \sim \mathrm{x}$
(3) Symmetry : $\mathrm{x} \sim \mathrm{y} \Rightarrow \mathrm{y} \sim \mathrm{a}$
(4) Transitivity : $\mathrm{x} \sim \mathrm{y} \text{and} \mathrm{y} \sim \mathrm{z} \Rightarrow \mathrm{x} \sim \mathrm{z}$

We then discussed how every equivalence relation ( $\mathrm{R}$ ) on $\mathrm{A}$ , partitions $\mathrm{A}$ into equivalence classes. Here is the example our textbooks gives us:

$\mathrm{P} = \{\text{all polynomials with real coefficents}\}$
$\mathrm{P} = \{\mathrm{a}_{\mathrm{n}}\mathrm{x}^{\mathrm{n}}+\mathrm{a}_\mathrm{x-1}}\mathrm{x}^{\mathrm{n-1}}+\text{...}+\mathrm{a}_{2}\mathrm{x}^{2}+\mathrm{a}_\mathrm{1}\mathrm{x}+\mathrm{a}_{\mathrm{o}} : \mathrm{a}_{\mathrm{i}}\in\mathbb{R}\}$

Define $\mathrm{R}$ (~) on $\mathrm{P}$ by:

$(\mathrm{f(x), g(x)})\in\mathbb{R}$ means…
$\mathrm{f(x)Rg(x)$ means…
$\mathrm{f(x)} \sim \mathrm{g(x)}$ means…

***** they all mean that the degree of $\mathrm{f(x)}$ are equal to the degree of $\mathrm{g(x)}$ *****

So the equivalence class of all degree two polynomials could be written as:

$[\mathrm{x}^{2}] = \{\text{all degree two polynomials\}$

A partition would be written as the union of the equivalence classes for each degree “n” polynomial:

$[28] \cup [\mathrm{x}] \cup [\mathrm{x}^{2}] \cup [\mathrm{x}^{3}] \cup \text{...}$

Well that’s all for now…at least for this blog entry.

Peace
Emily

The One With Pac-Man (Oct. 30)

November 15, 2015November 15, 2015 / tripletintegral / Leave a comment

Today we discussed equivalence statements and relations further.

Recall that relation statements can be written as follows:

$\text{R on a set A is }: \mathrm{R}\subseteq\mathrm{A x A}$

We then discussed equivalence classes which are ways of writing relations. This can be notated as follows:

$[\mathrm{x}] : = \{\mathrm{a}\in\mathrm{A}: \mathrm{aRx}\subseteq\mathrm{A}\}$

When something is an equivalence relation, the equivalence classes can be notated as:

$\mathrm{A} = \bigcup_{\mathrm{x}\in\mathrm{A}}=[\mathrm{x}]$

this equivalence classes are disjoint when:

$[\mathrm{x}]\cap[\mathrm{y}]\neq{0}$ $\Leftarrow\Rightarrow[\mathrm{x}] = [\mathrm{y}]$

We then got our fun math fact of the day. Since Pac-Man can go from the right-side to the left-side and from the top to the bottom, you can assume that the grid layout looks like this:

This means that if you fold the grid so the corresponding sides match up, it becomes clear that Pac-Man lives in a doughnut 🙂

Peace
Emily

The One Where We Start Relations (Oct. 28)

November 15, 2015November 15, 2015 / tripletintegral / Leave a comment

We began this class by revisiting the infamous cow proof. Specifically, we went over why it was wrong even though it was oddly convincing. The reasons are as follows

(1) Some people find that $\mathrm{S}_{\mathrm{k}}$ is wrong because $\mathrm{n} = 2$ was checked first.

(2) Others argue that $\mathrm{n} = 2$ wasn’t checked at all which would imply that induction can’t be trusted.

(3) Casey claims that our argument was $\forall\mathrm{K}+1 \neq 2$ which I agree makes the most sense.

It is very rare that induction proofs make it that difficult to figure out what the claim is, which is why induction proofs do actually work well when done correctly.

We then MOO-ved on to discussing relations. A relation is defined any subset $\mathrm{R}\subseteq\mathrm{A}\mathrm{X}\mathrm{B}$ . They’re called relations because the ordered pairs you get from the Cartesian Product relate $\mathrm{A}$ to $\mathrm{B}$ .

(Ex) $\mathrm{A} = \mathbb{Z}$ and $\mathrm{B} = \{\mathrm{a, b, c, d}\}$
One possible relation would be $\mathrm{R} = \{(0 , \mathrm{a}), (-10, \mathrm{b}), ( -1000, \mathrm{b}), (4, \mathrm{d})\}$

Relations from $\mathrm{A} \text{to} \mathrm{A}$ relations, or “relations on $\mathrm{A}$ are commonly studied although not all of them are meaningful. However, two examples of meaningful relations are the “equals relation” and the “greater than relation” which can be notated as follows:

(1) $\mathrm{R}=\{(\mathrm{x}, \mathrm{x}) : \mathrm{x}\in\mathbb{R}\}$

(2) $\mathrm{R}=\{(\mathrm{x}, \mathrm{y}) : \mathrm{x} - \mathrm{y} \in\mathbb{N}$

There are special kinds of relations called Equivalence Relations. These relations are special because they have three properties: reflexivity, symmetry, and transitivity. Here is how they can be notated:

(1) Reflexivity: $\mathrm{xRx} \forall\mathrm{x}\in\mathrm{A}$ .
(2) Symmetry: If $\mathrm{xRy}$ , then $\mathrm{yRx}$ .
(3) Transitivity: If $\mathrm{xRy}$ and $\mathrm{yRz}$ , then $\mathrm{xRz}$ .

Now to explain using Arrested Development characters because why not:

(1) Reflexivity: Buster is related to himself.
(2) Symmetry: If George Michael is related to Maeby, then Maeby is related to George Michael.
(3) Transitivity: If Buster is related to George Michael and George Michael is related to Maeby, then Buster is related to Maeby.

We then just spent the remainder of class working on our homework for that week.

Peace
Emily

The One With The Golden Ratio (Oct. 23)

November 15, 2015November 15, 2015 / tripletintegral / Leave a comment

Ok so I’m majorly behind on blog posts, but I am going to catch up today and then *hopefully* not fall behind again for the rest of the semester!

So according to my notes, the 23rd was a pretty short class. I think we probably just finished homework and listened to a brief lecture. I get the feeling we finished homework because in my notes I wrote “how the fuck do people come up with shit like #3?” with no further explaination. Stellar notes Em.

We then talked about continued fractions. We began with discussing the Golden Ratio, $\Phi$ , which is the “most irrational number in terms of continued fractions.” While the Golden Ratio is cool and all, some people have gone a bit over board in claiming the Golden Ratio applies to a bunch of random crap. Criminal Minds even had an episode where the Golden Ratio and the Fibonacci Spiral were the key to solving a case. It’s a little ridiculous but I actually really like that show. Here’s a clip because you doesn’t like getting distracted by YouTube:

People’s every expanding theories on $\Phi$ are cool and all but it’s probably just proof that the Illuminati are real. I mean how convincing is this image I stole from Google?

We then talked about the “Tower of Powers”. Much like the Disney ride “Tower of Terror,” it’s looks pretty intense at first, but once you get into it it’s not so bad. So here’s what the ToP looks like:

Say you have some number $\mathrm{x}$ that you’re just gonna continuously raise to some power to get another number:

$\mathrm{x}^{\mathrm{x}}^{\mathrm{x}}^{\mathrm{x}}^{\mathrm{x}}^{\mathrm{x}}^{text{...}}=\mathrm{y}$

Seems impossible right? Try looking at it this way:

$\mathrm{x}^{\mathrm{y}}=\mathrm{y}$
$\mathrm{x} = \mathrm{y}^{\frac{1}{\mathrm{y}}}$
$\Rightarrow(\sqrt{2})^{\sqrt{2}}^{\sqrt{2}}^{\sqrt{2}}^{\sqrt{2}}^{\text{...}} = 2$

It’s pretty cool stuff. Math is awesome.

Peace
Emily

The One With Homework 7 (Oct. 22)

October 22, 2015October 23, 2015 / tripletintegral / Leave a comment

Since I’ve been lacking on the blog front in recent weeks, I am going to blog about homework 7. Be warned if you’re reading this that I am very shaky (in my opinion at least) on proofs by induction.

(1) Find and verify a formula for the matrix $\displaystyle \left[\begin{array}{cc}1 & -1\\0 & 1\end{array}\right]^{\mathrm{n}}$ for all $\mathrm{n}\in\mathbb{N}$

We believe that the formula is $\displaystyle \left[\begin{array}{cc}1 & -\mathrm{n}\\0 & 1\end{array}\right]$ . We will attempt to verify this using proof by induction.
Observe what happens when $\mathrm{n}=1$

$\displaystyle \left[\begin{array}{cc}1 & -1\\0 & 1\end{array}\right]^{1} = \left[\begin{array}{cc}1 & -1\\0 & 1\end{array}\right]$ , which supports our formula.

Now, to establish a base case, we want to put things in terms of $\mathrm{k}$ . We will denote our base case as $\mathrm{S}_{\mathrm{k}}$

$\mathrm{S}_{\mathrm{k}} = \displaystyle \left[\begin{array}{cc}1 & -1\\0 & 1\end{array}\right]^{k} = \left[\begin{array}{cc}1 & -\mathrm{k}\\0 & 1\end{array}\right]$

For our inductive step, we will assume the above to be true. We now need to show that the formula holds true for $\mathrm{S}_{\mathrm{k}+1}$ which would mean that:

$\mathrm{S}_{\mathrm{k}+1} = \displaystyle \left[\begin{array}{cc}1 & -1\\0 & 1\end{array}\right]^{\mathrm{k}+1} = \displaystyle \left[\begin{array}{cc}1 & -(\mathrm{k}+1)\\0 & 1\end{array}\right]$

Note that we can actually rewrite this in a way that is beneficial for what we’re proving:

$\mathrm{S}_{\mathrm{k}+1} = \displaystyle \left[\begin{array}{cc}1 & -1\\0 & 1\end{array}\right]^{\mathrm{k}} * \displaystyle \left[\begin{array}{cc}1 & -1\\0 & 1\end{array}\right]^{1}$

Recall that based on our assumption, we know both of these to be true. If you use matrix multiplication and manipulation with these matrices you get the following matrix:

$\mathrm{S}_{\mathrm{k}+1} = \displaystyle \left[\begin{array}{cc}1 & -(\mathrm{k}+1)\\0 & 1\end{array}\right]$ , which is what we wanted.

$\therefore$ our formula $\displaystyle \left[\begin{array}{cc}1 & -\mathrm{n}\\0 & 1\end{array}\right]$ holds true. $\square$

(2) Prove the “power rule” using the “product rule”.

We assume the the product rule ( $(\mathrm{f}*\mathrm{g}^{'})+(\mathrm{g}*\mathrm{f}^{'})$ ) is true and that $\frac{\mathrm{d}}{\mathrm{dx}}(\mathrm{x})=1$ .
We are going to attempt to prove the power rule through proof by induction.

We already know that if $\mathrm{f}(\mathrm{x})=\mathrm{x}$ then $\mathrm{f}^{'}(\mathrm{x})=1$ and based on our understanding of exponents we know that this can be rewritten as $\mathrm{f}(\mathrm{x})=\mathrm{x}^{1}$ and using induction we know that in this case the derivative is still 1.

For our base case, again denoted $\mathrm{S}_{\mathrm{k}}$ , we want to express things in terms of $\mathrm{k}$

$\mathrm{S}_{\mathrm{k}} = \mathrm{f}(\mathrm{x}) = \mathrm{x}^{\mathrm{k}}$
$\Rightarrow \mathrm{f}^{'}(\mathrm{x}) = \mathrm{k}$

For our inductive step, we will assume that when $\mathrm{k}=1$ , the derivative is also 1.
We now want to show that $\mathrm{S}_{\mathrm{k}+1}$ is also true, which would mean that if $\mathrm{f}(\mathrm{x}) = \mathrm{x}^{\mathrm{k}+1}$ then $\mathrm{f}^{'}(\mathrm{x}) = (\mathrm{k}+1)*\mathrm{x}^{\mathrm{k}})$ .

Note that this can be rewritten in a way that allows us to use the product rule

$\Rightarrow \mathrm{f}(\mathrm{x}) = \mathrm{x}^{\mathrm{k}}*\mathrm{x}^{1}$

Now that we have rewritten this in the form of $\mathrm{f}*\mathrm{g}$ we can use the product rule to find the derivative. Recall that based on our assumptions we know that both $\mathrm{f}$ and $\mathrm{g}$ are in fact true and we know their derivatives.

Let $\mathrm{f} = \mathrm{x}^{\mathrm{k}}$ and let $\mathrm{g} = \mathrm{x}^{1}$

$\Rightarrow (\mathrm{f}\mathrm{g}^{'})+(\mathrm{g}*\mathrm{f}^{'})$
$\Rightarrow \mathrm{x}^{\mathrm{k}}(1) + \mathrm{x}^{1}(\mathrm{k})$
$\Rightarrow (\mathrm{k}+1)*(\mathrm{x}^{\mathrm{k}}+\mathrm{x}^{1})$
$\Rightarrow (\mathrm{k}+1)*(\mathrm{x}^{\mathrm{k}})$ , which is what we WTS.

$\therefore$ the power rule if valid. $\square$

Peace
Emily

The One With Even More Induction (Oct. 21)

October 22, 2015October 22, 2015 / tripletintegral / Leave a comment

Today we continued our work with proofs by induction. I’m gonna be honest, I am NOT a fan of induction! I’m hoping that eventually I’ll have an “ah-ha” moment where it clicks in my brain, but until that happens I’m struggling with understanding what exactly to use as a base case and how to prove that if 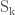$\mathrm{S}_{\mathrm{k}}$ is true, then so is $\mathrm{S}_{\mathrm{k}+1}$ . We began class by learning how you can use a contrapositive approach when using induction. To demonstrate this, Casey wrote out the goal of “standard” induction and then the goal of “contrapositive” induction:

Standard
$\mathrm{S}_{1}\Rightarrow\mathrm{S}_{2}\Rightarrow\mathrm{S}_{3}\Rightarrow\mathrm{S}_{4}\Rightarrow\text{...}\Rightarrow\mathrm{S}_{\mathrm{k}}\Rightarrow\mathrm{S}_{\mathrm{k}+1}\Rightarrow\text{...}$

Contrapositive
$(\sim\mathrm{S}_{1})\Leftarrow(\sim\mathrm{S}_{2})\Leftarrow(\sim\mathrm{S}_{3})\Leftarrow\text{...}\Leftarrow(\sim\mathrm{S}_{\mathrm{k}})\Leftarrow(\sim\mathrm{S}_{\mathrm{k}+1})\Leftarrow\text{...}$

We also learned that the contrapositive approach to induction is referred to as the proof by least counter-example method. I liked writing the goals out in this notation because while I don’t really understand how to make induction work, this helps give me a visual representation of what I am trying to do. I assuming that like the “normal” contrapositive approach to proofs, this one can only be used when we’re given an “if-then” statement.

We then moved on to discussing the Fundamental Theory of Arithmetic, which is arguably the most important proof we’ve learned to date. The theorem says that any number can be written as the product of two prime numbers. For example, 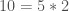$10 = 5* 2$ and $36 = 2^{2} * 3^{2}$ . In more math-y terms, this can be expressed as:

$\forall\mathrm{n}\in\mathbb{N},\mathrm{n}>1, \mathrm{n} \text{has } ! \text{prime factorization such that }\mathrm{n}=\mathrm{p}_{1}^{\alpha} * \mathrm{p}_{2}^{\alpha}*\text{...}*\mathrm{p}_{\mathrm{n}^{\alpha}}$

We can read about this on page 164 in our textbook, which I have done, but still don’t quite understand it, so I’m going to look at it more in the near future in the hopes I can understand it better. We were told before reading it that the three things we need to prove this are: (1) strong induction (2) cases and (3) proof by least counter-example.

We then went over a proof about cows that basically shows that the induction method could actually be complete bullshit.

The proof basically says that all cows are brown, which obviously isn’t true, but the proof makes a pretty convincing argument. It’s just a tad bit trippy. Instead of rewriting the proof just like we did it in class, I will replace the cows with something a little more exciting…LIGHTSABERS! In honor of my boy Obi-Wan, I am going to claim that all lightsabers are blue.

Proposition
All lightsabers are blue.

Proof
Base case: {one blue lightsaber}
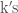Inductive step: Suppose whenever someone has a set of $\mathrm{k}$ lightsabers, that all $\mathrm{k's}$ are known.
WTS that in any set of $\mathrm{k}+1$ lightsabers, all $\mathrm{k}+1$ lightsabers are blue.
Let $\mathrm{M}$ be any set with $\mathrm{k}+1$ lightsabers.
Consider that $\mathrm{A}=\mathrm{B}\cup\{\text{last lightsaber}\}$
By assumption this would mean that all lightsabers in 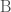$\mathrm{B}$ are blue.
Consider 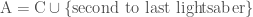$\mathrm{A}=\mathrm{C}\cup\{\text{second to last lightsaber}\}$
$\Rightarrow(\mathrm{C}=\{\mathrm{lightsaber}_{1}, \mathrm{lightsaber}_{2},...,\mathrm{lightsaber}_{\mathrm{k-1}}, \mathrm{lightsaber}_{\mathrm{k}+1}\})$
$\Rightarrow|\mathrm{C}|=\mathrm{K}$
Thus, our hypothesis implies that the lightsabers in $\mathrm{C}$ are blue.
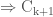$\Rightarrow\mathrm{C}_{\mathrm{k}+1}$ is blue
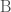$\Rightarrow$ all lightsabers in $\mathrm{B}$ are blue. $\square$

*****the base case could have been something like “the same color” instead of blue*****

We know that this isn’t true because there are other options for lightsabers (purple, green, red,…) but the proof above is still a relatively solid proof. This is why some mathematicians are skeptical about using induction to prove things. However, I can see how induction is an important way to think about proofs even if I don’t yet fully understand it.

After this, we just spent the rest of class working on homework, which I didn’t really make much headway on. I plan on blogging more about this later, so in order to avoid repeating myself, that’ all for now.

Peace
Emily

The One With Induction (Oct. 19)

October 19, 2015October 19, 2015 / tripletintegral / Leave a comment

First off, sorry about my lack of blog posts in the past week. Hopefully I’m all caught up now!

Today we did more with induction by doing some of the problems that I’m assuming will be on our homework. I’ve inserted pictures of what we did in class, but will also elaborate on and correct them as need be (*****I will come back and to do this later, for now, I just want to get something posted*****) in this particular post.

I have done proofs by induction before in Linear Algebra although we didn’t really go over what that meant at the time. I was hoping that since I’ve seen it before, I would be okay at it. However, after today I’m still struggling with it a bit. I understand how it supposed to work, what I struggle with the most is how much you’re actually allowed to assume. For example, in the second problem, I don’t know if we’re also allowed to assume that the Power Rule is true or if we have to prove that separately. Any advice Casey?

Peace
Emily

	tripletintegral on The One With The POW (Oct.…
	maryzajac on The One With The POW (Oct.…
	tripletintegral on The One Where We Review For Te…
	d0mo on The One Where We Review For Te…
	d0mo on The One With A Proof By Contra…

Triplet Integral

A blog about the adventures of FOM

Uncategorized

The One Where We Get Funky (Nov. 9)

The One With Partitions and Well-Defined Things (Nov. 6)

The One With Homework and the POW (Nov. 4)

The One With The Wiggles (Nov. 2)

The One With Pac-Man (Oct. 30)

The One Where We Start Relations (Oct. 28)

The One With The Golden Ratio (Oct. 23)

The One With Homework 7 (Oct. 22)

The One With Even More Induction (Oct. 21)

The One With Induction (Oct. 19)